ABACUS: MYSTERY OF THE BEAD |
 Raíces Cuadradas; Método de Fukutaro Kato
(contribución de Edvaldo Siqueira)
Raíces Cuadradas; Método de Fukutaro Kato
(contribución de Edvaldo Siqueira)
El siguiente es un método utilizado por el profesor Fukutaro Kato, un maestro japonés de soroban que vivió en Brasil en la década de 1960. El método fue publicado en el libro del Profesor, SOROBAN pelo Método Moderno que, traducido del portugués, significa: SOROBAN por el Método Moderno.
Intentaré exponer las ideas de Kato para extraer la raíz cuadrada. Si no recuerdo mal, Kojima menciona este método de pasada. Antes del método en sí, es útil comprender los tres conceptos siguientes.
I) LA MITAD DE UN NÚMERO AL CUADRADO (Aunque se gana velocidad aprendiendo de memoria la siguiente tabla, su memorización no es estrictamente necesaria mientras se extrae la raíz cuadrada.)
Número Cuadrado Semi-cuadrado 1 --------- 1 --------- 0.5 2 --------- 4 --------- 2.0 3 --------- 9 --------- 4.5 4 --------- 16 --------- 8.0 5 --------- 25 --------- 12.5 6 --------- 36 --------- 18.0 7 --------- 49 --------- 24.5 8 --------- 64 --------- 32.0 9 --------- 81 --------- 40.5 |
II) CÓMO REDUCIR A LA MITAD UN NÚMERO EN EL SOROBAN (SIN DESPLAZAR EL ORDEN)
Aquí no queremos desplazar el orden de los números en el soroban. Multiplicar por 0.5 es lo mismo que dividir por 2 (para algunos puede ser más fácil multiplicar que dividir. Para los mejores resultados use la técnica de multiplicación moderna.) Como ejemplo, supongamos que tenemos el número 325, como se muestra abajo en D,E y F. Multiplplicando 325 x 0.5 = 1625.
A B C D E F G H 0 0 0 3 2 5 0 0 |
A B C D E F G H 0 0 0 1 6 2 5 0 |
Como alternativa, podemos pensar de la siguiente forma: En lugar de multiplicar por 0.5 sustraemos la mitad de cada número. Comenzando por la derecha y trabajando hacia la izquierda, restar ½ de 5 en F dejando 2.5 en FG. Restar ½ de 2 en E dejandolo en 1. Finalmente restar ½ de 3 en D dejando 1.5 en D y E. Esto conduce al resultado deseado 1625 en las varillas DEFG.
III) DISPONER LOS NÚMEROS EN EL SOROBAN
En cuanto al modo de disponer los números sobre el soroban, el Profesor Fukutaro lo explica del siguiente modo:
a) El radicando debe ponerse de modo que su unidad caiga en una varilla unidad
b) Cuando un número no es un cuadrado perfecto, se debe prestar atención
a
que la unidad del resto siempre debe caer también en dicha varilla unidad.
c) Para situar la raíz cuadrada (resultado), deberán seguirse los siguientes
principios:
ci) Si el radicando sólo consta de grupos completos de dos dígitos,
(como 1225), disponer el dígito más alto de su raíz (3) exactamente en la
primera columna de la izquierda adyacence al radicando
cii) Si el radicando tiene un grupo incompleto de dos dígitos
(como 15129), saltar una varilla a la izquierda para situar el dígito
de mayor orden de la raíz (1 1 en este caso).
Con estas directrices (I, II y III) en mente, tratemos de encontrar la raíz cuadrada de *1225*
Antes de continuar, puede ser útil visitar estos enlaces: |
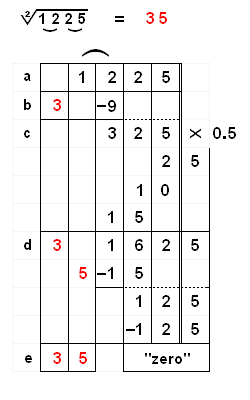
Ejemplo 1: \/ 1225 = 35
|
|
a) Separar mentalmente el número 1225 en grupos de 2 números cada uno, 12 25. b) Mirar el primer grupo (12). Encontrar el cuadrado perfecto más grande que sea menor o igual a 12. La respuesta es 3. (Elevar al cuadrado este 3, 3^2= 9). Restar 9 de 12. Nos queda 325. c) Encontrar la mitad de 325 (multiplicar por 0.5). El resultado es 162.5 d) Para encontrar el segundo dígito, dividir 16 entre 3. El entero más grande es 5. d) Multiplicar el primer dígito calculado por el segundo. (3 x 5) y restar el producto 15 de 16. Nos queda 12,5. e) Restar el semi-cuadrado de 5: 12.5 (consultar la tabla de arriba si aún no la hemos memorizado.) Nos queda cero ("zero" en la figura) ¡Eso es todo! Acabamos de encontrar la raíz cuadrada 35. |
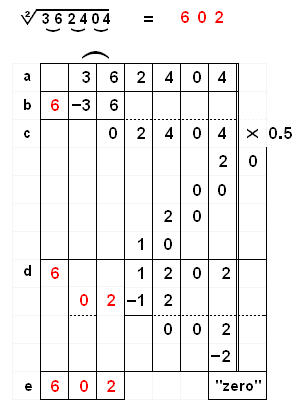
Ejemplo 2: \/ 362404 = 602
|
|
a) Separar mentalmente el número 362404 en grupos de 2 números cada uno, 36 24 04. b) Mirar el primer grupo (36). Encontrar el cuadrado perfecto más grande que sea menor o igual a 36. La respuesta es 6. (Elevar al cuadrado este 6 6^2=36). Restar 36 del primer grupo, quedando 02404. c) Encontrar la mitad de 2404 (multiplicar por 0.5). El resultado es 1202 d) Para encontrar el segundo dígito, dividir 1 por 6. No se puede hacer, así que pasar a dividir 12 entre 6. El entero más grande es 2. d) Multiplicar el primer dígito calculado por el segundo (6 x 2) y restar el producto 12 de 12. Nos queda 2. e) Restar el semi-cuadrado de 2: 2 (consultar la tabla). Nos queda cero El resultado del problema es 602. |
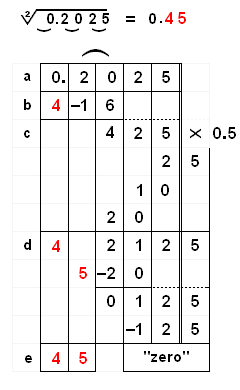
Ejemplo 3: \/ 0.2025 = 0.45
|
|
a) Separar mentalmente el número 0.2025 en grupos de 2 números cada uno, 0 20 25. b) Aquí el primer grupo a trabajar es 20. Su cuadrado perfecto más grande es 4. (El cuadrado de este 4 es 16). Restar 16 del primer grupo, quedando 425. c) Encontrar la mitad de 425 (multiplicar por 0.5). El resultado es 212.5 d) Para encontrar el segundo dígito, dividir 21 entre 4. EL mayor entero es 5. d) Multiplicar el primer dígito calculado por el segundo (4 x 5) y restar el producto 20 de 21. Nos queda 2. e) Restar el semi-cuadrado de 5: 12.5 (consultar la tabla). Nos queda cero El resultado del problema es 0.45 |
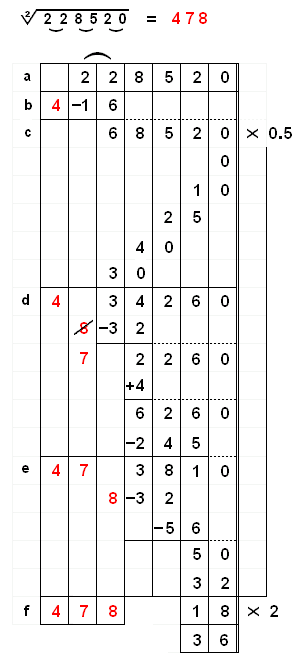
Ejemplo 4: \/ 228520 = 478
*** Este es un ejemplo interesante porque muestra lo fácil que es revisar un resultado en caso de error.***
|
|
a) Separar mentalmente el número 228520 en grupos de 2 números cada uno, 22 85 20. b) Sabemos que el primer número del resultado ha de ser 4. (Elevar al cuadrado 4^2 =16). Restar 16 del primer grupo 22, quedando 68520. c) Encontrar la mitad de 68520 (multiplicar por 0.5). El resultado es 34260 d) Para encontrar el segundo dígito, dividir 34 entre 4. El mayor entero es 8. Multiplicar 4 x 8 y restar el producto 32 de 34. Ahora el método requiere sustraer el semicuadrado de 8, (8 *8)/2 = 64 /2 = 32. Pero he aquí el problema. *Con un resto de sólo 22, no podemos sustraer 32.* ¿La solución? Revisar el resultado de 8 a 7 y devolver 4, quedando 6260. Ahora podemos restar el semicuadrado de 7 = 24.5 (ver tabla superior). Nos queda 3810 e) Para encontrar el tercer dígito, dividir 38 entre 4. Si elegimos 9 tendremos que revisar nuestra respuesta (como hicimos en el paso d) porque no habrá suficiente resto para continuar con el siguiente paso. Elegir 8 en su lugar. Multiplicar 8 x 4 y restar 32 de 38. Luego multiplicar 7 x 8 y resta su producto 56 dejando 50. Restar el semicuadrado de 8 = 32 (ver la tabla anterior), dejando 18. f) Aunque este problema podría continuarse más allá, hasta aquí nos lleva el Profesor. En lugar de seguir, nos muestra qué hacer con el resto. En el paso c) multiplicamos por 0.5 (dividimos por 2). Ahora necesitamos multiplicar 18 por 2. (18 x 2 = 36) El resultado del problema es 478, resto 36 |
MÁS EJEMPLOS:
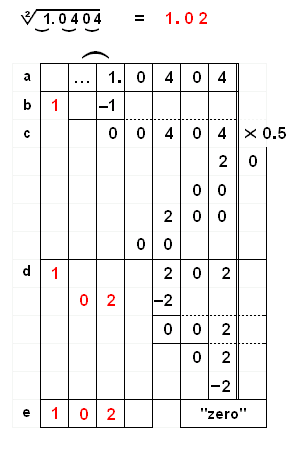 |
 |
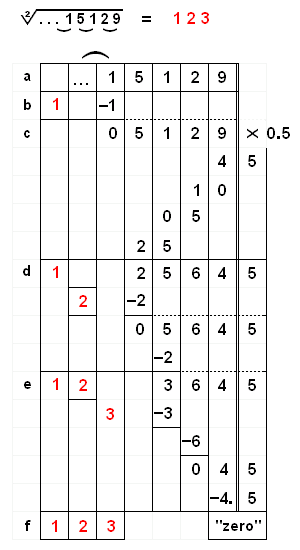 |
 |
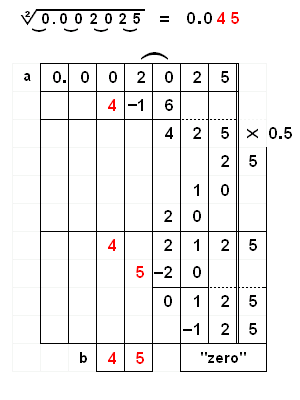 |
Artículo traducido del original en lengua inglesa
por Jesús Cabrera - gmail: jccsvq
(2022)
▪
Técnicas Avanzadas para el Ábaco
▪
Find the Square Root of 2 to seven decimal places
PÁGINA IMPRIMIBLE
| Edvaldo Siqueira Rio de Janeiro, Brazil |
Totton Heffelfinger |