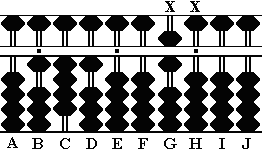ABACUS: MYSTERY OF THE BEAD
The Bead Unbaffled - An Abacus Manual
![]() OBTENCIÓN DE LA RAÍZ CUADRADA DE 2 CON SIETE DECIMALES
OBTENCIÓN DE LA RAÍZ CUADRADA DE 2 CON SIETE DECIMALES
Muchas veces he deseado que el profesor Kato hubiera ido un poco más lejos e ilustrado su técnica usando uno o dos ejemplos en los que se obtuviera un resultado decimal largo a partir de un número entero. Aquí presento un buen ejemplo de tales raíces cuadradas. Debido al largo resultado decimal, nos haremos una idea bastante buena de la técnica así como del modo en que se deben colocar los números en el soroban.
El método de Kato para obtener la raíz cuadrada de un número está bien documentado. Por favor estúdielo en primer lugar. A excepción de los primeros pasos, este ejemplo solo mostrará imágenes del soroban después de completar cada una de las operaciones. Los diagramas pueden ser útiles como guía para ayudar a evaluar la comprensión de la técnica.
Un par de cosas a Recordar:
i) En lo que sigue, es importante recordar que los dígitos que forman el radicando se dividen en grupos de dos. Al buscar la raíz cuadrada de 2, el primer grupo es 02. Los grupos posteriores se emparejan como 00 00 00 y así sucesivamente.
ii) El método del Prof. Kato requiere restar 1/2 de un número al cuadrado (página principal). Como resultado, a veces entran en juego fracciones como 0.5, 4.5, 12.5, etc. Recuerde, debido a que es una fracción, al restar 0.5 la operación siempre llevará otro 0.5 al siguiente par de números (ver los pasos 1b y 3b para aclaraciones).
Para ilustrarlo, realizaré los primeros pasos para encontrar la raíz cuadrada de 2.
En este paso el grupo es 02 en las columnas CD con el siguiente par 00
(XX) en las columnas EF.
|
Paso 1: Encontrar la raíz cuadrada de 2. Ponemos 2 en la columna D. El grupo en este punto es 02 en las columnas CD y el siguiente grupo 00 en las columnas EF. (Fig. A) |
Fig. A |
|
|
Paso 1a: Buscamos el mayor cuadrado perfecto que sea menor o igual a 2. La respuesta es 1. Colocamos 1 en la barra. B Elevamos al cuadrado el 1 en B (1 x 1 = 1), restamos 1 de 2 en la columna D quedando 1. (Fig. B) |
Fig. B |
|
|
Paso 1b: Restamos *la mitad* de 1 de la columna D. Esto lleva 0.5 a la varilla E en el siguiente grupo. (Fig. C)
|
Fig. C |
|
En cada uno de los pasos de división a continuación, debe quedar suficiente resto como para restar *la mitad* de la respuesta al cuadrado. Veámoslo en este siguiente paso.
|
Paso 2: Dividimos 5 en E por 1 en B. Parece que el cociente debería ser 5, pero la técnica requiere dejar suficiente resto. Elegimos 4 en lugar de 5. El resto resultante nos permitirá completar el Paso 2a (ver abajo). Ponemos el cociente 4 en la columna C. Multiplicamos el 4 en C por el 1 en B y sustraemos el resultado del 5 en la columna E. Esto deja 1. (Fig. D)
|
Fig. D |
|
|
Paso 2a: Elevamos al cuadrado el 4 en la columna C (4 x 4 = 16) y restamos *la mitad* (8) de las columnas EF. Esto deja la respuesta parcial 1.4 en las barras BC y un resto de 2 en la barra F. (Fig. E) |
Fig. E |
|
En este paso añadimos otro grupo de 00 (XX), Esta vez las columnas GH.
|
Paso 3: Dividimos el 2 en F por el 1 en B y ponemos el cociente 1 en la columna D. Multiplicamos el 1 en D por el 1 en B (1 x 1 = 1). Sustraemos 1 del 2 en la columna F quedando 1. (Fig. F) |
Fig. F |
|
|
Paso 3a: Multiplicamos el 1 en la columna D por el 4 en C (1 x 4 = 4). Restamos 4 de las barras FG. Esto deja 6 en la barra G. (Fig. G)
|
Fig. G |
|
|
Paso 3b: Elevamos al cuadrado el 1 en la barra D (1 x 1 = 1) y restamos *su mitad* (0.5) del resto. Esto deja el resultado parcial 1.41 en las barras BCD y el resto 595 en las barras GHI. (Fig. H) **Al restar 0.5 (no un número entero) de la columna H, se suma 0.5 al siguiente par de números, en este caso, a la columna I. ** |
Fig. H |
|
En este paso añadimos otro grupo de 00 (XX), Esta vez las columnas IJ.
|
Paso 4: Dividimos el 5 en G por el 1 en B. Ponemos el cociente 4 en la columna E. Multiplicamos el 4 en E por el 1 en B y restamos el resultado de la columna G. (Fig. I) |
Fig. I |
|
|
Paso 4a: Multiplicamos el 4 en E por el 4 en C y restamos 16 de las barras GH. (Fig.J)
|
Fig. J |
|
|
Paso 4b: Multiplicamos el 4 en E por el 1 en D y restamos 04 de las columnas HI. (Fig. K)
|
Fig. K |
|
|
Paso 4c: Elevamos al cuadrado el 4 en la columna E (4 x 4 = 16) y restamos *su mitad* (8) de las barras IJ. Esto deja la respuesta parcial 1.414 sobre las columnas BCDE y el resto 302 sobre las columnas JIJ. (Fig. L) |
Fig. L |
|
En este punto, el problema se ha resuelto con tres decimales, lo que da una idea bastante clara de cómo funciona la técnica. Para continuar, simplemente agregamos más pares de 00 (XX), completamos la división y restamos *la mitad* del número al cuadrado como se muestra arriba.
Los siguientes diagramas llevan el ejemplo a siete lugares decimales. El proceso comienza desde el principio y muestra el soroban después de completar cada etapa. Utilice los diagramas como guía para comprobar la precisión.
LOS DIAGRAMAS:
Problem: Find the square root of 2
 Fig.1
Fig.1
 Fig.2
Fig.2
 Fig.3
Fig.3
 Fig.4
Fig.4
 Fig.5
Fig.5
 Fig.6
Fig.6
 Fig.7
Fig.7
 Fig.8
Fig.8
 Fig.9
Fig.9
Por supuesto, el problema podría continuar, pero con 7 decimales en la respuesta, este es un buen lugar para detenerse.
Observe las varillas L a S. En este punto llevan el resto 0.000000088208875. Para encontrar el resto verdadero, la técnica de Kato requiere multiplicar por 2. Multiplicar 0.000000088208875 x 2 = 0.00000017641775
El resultado es 1.4142135 en las columnas B hasta I con un resto de 0.00000017641775
Elevamos al cuadrado el resultado en el soroban
1.4142135 * 1.4142135 = 1.99999982358225
Sumamos el resto a lo anterior
1.99999982358225
+ 0.00000017641775
2.00000000000000 <=== Respuesta 2, que es el problema original
18 de Marzo de 2006
Como nota personal, escribir esta página hace 3 meses me obligó a estudiar concienzudamente la técnica del Prof. Kato. Para poder ilustrarla, realmente tenía que entenderla. Desde entonces, me he sentido cada vez más cómodo con ella. Me he beneficiado de la práctica cotidiana usando ejemplos aleatorios de diferentes tamaños y, habitualmente, resolviendo el problema con cinco o seis decimales. La técnica funciona muy bien y es muy eficiente. Vale la pena tomarse el tiempo para entenderla. En mi opinión, no existe método mejor.
- TPH marzo de 2006