 Técnicas Tradicionales de Multiplicación para el Suanpan Chino - La Cuenta
Extra y la Cuenta Suspendida
Técnicas Tradicionales de Multiplicación para el Suanpan Chino - La Cuenta
Extra y la Cuenta Suspendida
El Suanpan, o ábaco chino, estuvo en uso en China durante dos o tres siglos antes de viajar a Japón a finales del siglo XVI. A diferencia del Soroban japonés actual, que ha evolucionado para convertirse en un instrumento con una estructura de 1/4 de cuentas, el Suanpan ha conservado su estructura clásica de 2/5 de cuentas: 2 cuentas por encima de la barra central y 5 cuentas por debajo. Las técnicas que se describen a continuación pueden ofrecer una idea de por qué esto podría ser así.
Estas técnicas son más antiguas y difieren de los métodos chinos modernos en que el orden de multiplicación y suma de productos al ábaco es diferente. Estas técnicas podrían incluso ser reconocibles para una generación anterior en Japón, muchos de los cuales crecieron aprendiendo métodos más antiguos. Las nuevas ideas y los cambios en la composición física del ábaco japonés a principios del siglo pasado provocaron cambios en la forma en que muchos japoneses modernos hacen su trabajo con el ábaco. El aprender estas técnicas chinas, no solo permite una mejor comprensión del uso del ábaco, sino que también brinda una visión más profunda del instrumento y el pensamiento tras su desarrollo y uso.
- La técnica de la Cuenta Extra usa la cuenta superior más alta y tiene un valor de 5. (ver Ejemplo 3: Paso 3 abajo)
- La técnica de la Cuenta Suspendida también utiliza la cuenta superior más alta, pero en este caso se coloca a la mitad de la varilla para que la cuenta no toque ni el marco de arriba ni la cuenta de abajo; tiene un valor de 10. (ver Ejemplo 4: Pasos 3 y 4 abajo)
Antes de comenzar con estas técnicas, sería útil tener una buena comprensión de las técnicas de suma y multiplicación descritas en: Ábaco: El Misterio de la Cuenta
La columna unidad y los decimales
Esta técnica hace que trabajar con decimales y la columna unidad sea maravillosamente fácil. Sólo hay que contar el número de dígitos a la izquierda del punto decimal o los ceros a su derecha en el multiplicador para localizar la barra unidad del resultado.
Multiplicación y Desplazamiento de la Columna Unidad
Si el multiplicador es....
1.003..... un dígito a la izquierda - la columna unidad se desplaza 1 barra a la derecha.
45.03..... dos dígitos a la izquierda - la columna unidad se desplaza 2 barras a la derecha.
0.75....... sin dígitos a la izquierda, sin ceros a la derecha del punto, la columna unidad *no* se desplaza.
0.0125... un cero a la derecha del punto: la columna unidad se desplaza 1 barra hacia la izquierda.
0.0036... dos ceros a la derecha del punto - la columna unidad se desplaza 2 barras a la izquierda... etc.
|
Suanpan y los Decimales
- Multiplicación: |
Las técnicas de multiplicación chinas tradicionales difieren de las técnicas japonesas de
multiplicación . Especialmente diferente
es el orden en que multiplicamos los números. Antes de pasar a las técnicas de
la Cuenta Extra y la Cuenta Suspendida, veremos dos ejemplos sencillos que ayudarán
a ilustrar cómo funciona este método de multiplicación tradicional.
Ejemplo 1: 456 x 23 = 10,488
El orden de la multiplicación:
Consulte la Fig. 1 a continuación. El orden de operación es el siguiente;
▪ Columna H x B
x A. Nota: el multiplicando en la barra H
cambia para convertirse en parte del producto.
▪ Columna G x B
x A. Nota: el multiplicando en la barra G
cambia para convertirse en parte del producto.
▪ Columna F x B
x A. Nota: el multiplicando en la barra F
cambia para convertirse en parte del producto.
Paso 1: Tomamos H como columna unidad. Ponemos el multiplicando 456 en las varillas FGH y el multiplicador 23 en AB. El multiplicador tiene dos dígitos enteros por lo que la varilla unidad del resultado estará dos posiciones a la derecha de la del multiplicando, esto nos lleva a la columna J. (Fig.1)
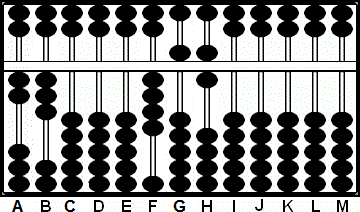 Fig.1 Fig.1 |
Paso 1
A B C D E F G H I J K L M
2 3 0 0 0 4 5 6 0 0 0 0 0
|
Paso 2: Multiplicamos 6 por 3 y sumamos 18 a las varillas IJ. (Fig. 2)
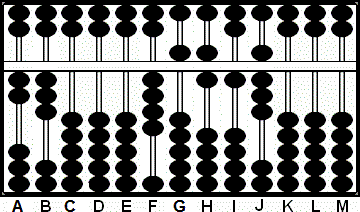 Fig.2 Fig.2 |
Paso 2
A B C D E F G H I J K L M
2 3 0 0 0 4 5 6 0 0 0 0 0
+ 1 8
2 3 0 0 0 4 5 6 1 8 0 0 0
|
Paso 3: Multiplicamos 6 por 2 y sumamos 12 a las varillas HI. Nótese que lo que era
el 6 del multiplicando en H ha cambiado ahora a 1. (Fig. 3)
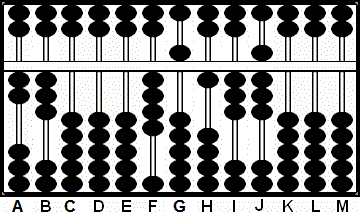 Fig.3 Fig.3 |
Paso 3
A B C D E F G H I J K L M
2 3 0 0 0 4 5 6 1 8 0 0 0
+ (1)2
2 3 0 0 0 4 5 1 3 8 0 0 0
|
Paso 4: Multiplicamos 5 por 3 y sumamos 15 a las varillas HI. (Fig. 4)
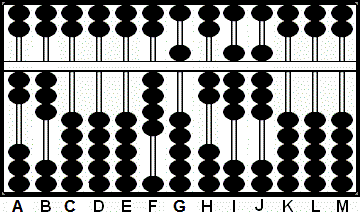 Fig.4 Fig.4 |
Paso 4
A B C D E F G H I J K L M
2 3 0 0 0 4 5 1 3 8 0 0 0
+ 1 5
2 3 0 0 0 4 5 2 8 8 0 0 0
|
Paso 5: Multiplicamos 5 por 2 y sumamos 10 a las varillas GH. Nótese que lo que era
el 5 del multiplicando en G ha cambiado ahora a 1. (Fig. 5)
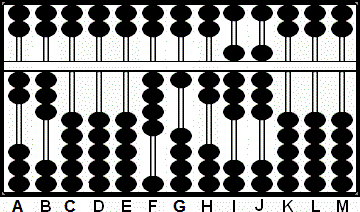 Fig.5 Fig.5 |
Paso 5
A B C D E F G H I J K L M
2 3 0 0 0 4 5 2 8 8 0 0 0
+ (1)0
2 3 0 0 0 4 1 2 8 8 0 0 0
|
Paso 6: Multiplicamos 4 por 3 y sumamos 12 a las varillas GH. (Fig. 6)
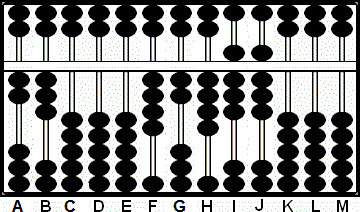 Fig.6 Fig.6 |
Paso 6
A B C D E F G H I J K L M
2 3 0 0 0 4 1 2 8 8 0 0 0
+ 1 2
2 3 0 0 0 4 2 4 8 8 0 0 0
|
Paso 7 y resultado: Multiplicamos 4 por 2 y sumamos 08 a las varillas FG.
Nótese una vez más el cambio; lo que originalmente era el el 4 del multiplicando en F
cambia a 0 y después a 1 tras sumar 8 a 2 en la varilla G. Esto deja 10,488
como resultado en las varillas F - J.
(Fig. 7)
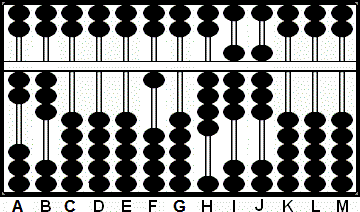 Fig.7 Fig.7 |
Paso 7
A B C D E F G H I J K L M
2 3 0 0 0 4 2 4 8 8 0 0 0
+ (0)8
2 3 0 0 0 1 0 4 8 8 0 0 0
|
Ejemplo 2: 347 x 276 = 95,772
El Orden de Multiplicación:
Consulte la Fig. 1 a continuación. El orden de operación es el siguiente;
▪ Columna H x B
x C x
A. Nota: el multiplicando en la barra H
cambia para convertirse en parte del producto.
▪ Columna G x B
x C x A. Nota: el multiplicando en la barra G
cambia para convertirse en parte del producto.
▪ Columna F x B
x C x A. Nota: el multiplicando en la barra F
cambia para convertirse en parte del producto.
Paso 1: Tomamos la columna H como varilla unidad. Disponemos el multiplicando
347 en las columnas FGH y el multiplicador 276 en ABC. El multiplicador tiene
tres dígitos a la izquierda del punto decimal por lo que la columna unidad del producto
estará tres posiciones a la derecha de H, en la columna K.
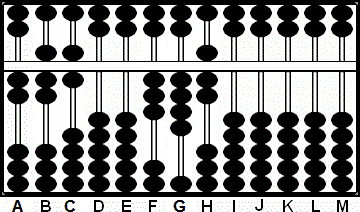 Fig.1 Fig.1 |
Paso 1
A B C D E F G H I J K L M
2 7 6 0 0 3 4 7 0 0 0 0 0
|
Paso 2: Multiplicamos 7 por 7 y sumamos 49 a las columnas IJ.
2a: Multiplicamos 7 por 6 y sumamos 42 a las columnas JK.
2b: Multiplicamos 7 por 2 y sumamos 14 a las columnas HI. Nótese que lo que era
el 7 del multiplicando en H ha cambiado ahora a 1. (Fig. 2)
 Fig.2 Fig.2 |
Paso 2
A B C D E F G H I J K L M
2 7 6 0 0 3 4 7 0 0 0 0 0
+ 4 9
+ 4 2
+ (1)4
2 7 6 0 0 3 4 1 9 3 2 0 0
|
Paso 3: Multiplicamos 4 por 7 y sumamos 28 a las columnas HI.
3a: Multiplicamos 4 por 6 y sumamos 24 a las columnas IJ.
3b: Multiplicamos 4 por 2 y sumamos 08 a las columnas GH. Nótese que lo que era
el 4 del multiplicando en G ha cambiado a 0 y después a 1 tras sumar 8 a
la columna H. (Fig. 3)
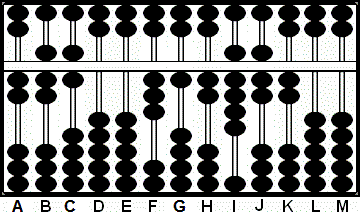 Fig.3 Fig.3 |
Paso 3
A B C D E F G H I J K L M
2 7 6 0 0 3 4 1 9 3 2 0 0
+ 2 8
+ 2 4
+ (0)8
2 7 6 0 0 3 1 2 9 7 2 0 0
|
Paso 4: Multiplicamos 3 por 7 y sumamos 21 a las columnas GH.
4a: Multiplicamos 3 por 6 y sumamos 18 a las columnas HI.
4b y resultado: Multiplicamos 3 por 2 y sumamos 06 a las columnas FG.
Nótese el cambio una vez más; lo que era el 3 del multiplicando en F cambia a 0.
Esto nos deja 95,772 en las columnas G - K como resultado. (Fig. 4)
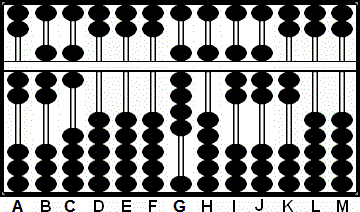 Fig.4 Fig.4 |
Paso 4
A B C D E F G H I J K L M
2 7 6 0 0 3 1 2 9 7 2 0 0
+ 2 1
+ 1 8
+ (0)6
2 7 6 0 0 0 9 5 7 7 2 0 0
|
Ejemplo 3:
"La Cuenta Extra"
Cuando se trata de sumar los productos en el ábaco, la mayor parte de las técnicas requieren el uso de números complementarios. En los ejemplos que siguen los usaremos siempre que podamos. Sin embargo, en el Paso 3 (ver abajo) el uso de números complementarios podría resultar confuso.
189 x 576 = 108,864
Paso 1: Disponemos el multiplicador 576 en DEF y el multiplicando 189 en HIJ. (Fig.1)
|
|
Paso 1
A B C D E F G H I J K L M
0 0 0 5 7 6 0 1 8 9 0 0 0
|
Paso 2: Multiplicamos el 9 en la varilla J por el 7 en E y sumamos el producto 63 en KL.
2a: Multiplicamos el 9 en la varilla J por el 6 en F y sumamos el producto 54 en LM
2b: Multiplicamos el 9 en la varilla J por el 5 en D, quitamos el 9 de J y sumamos el producto 45 en JK . Esto deja 185184 en las columnas H - M. (Fig.2)
|
|
Paso 2
A B C D E F G H I J K L M
0 0 0 5 7 6 0 1 8 9 0 0 0
+ 6 3 Paso 2
+ 5 4 Paso 2a
(4)5 Paso 2b
0 0 0 5 7 6 0 1 8 5 1 8 4
|
Aquí es donde usamos la Cuenta Extra. En este punto vamos a
multiplicar el 8 en la barra I por el 7 en E. Si fuéramos a hacer un acarreo
aquí, tendríamos que cambiar el 8 por 9 pero esto sería confuso. (Especialmente porque
es el 8 el que se multiplicará por cada uno de los dígitos del multiplicador).
Como hay una cuenta adicional de valor 5 disponible en J, la usaremos para evitar confusiones.
Paso 3:
Multiplicamos el 8 en la barra I por el 7 en E y sumamos el producto 56
en JK, dejando 1 8 "10" 7 8 4 en las columnas H - M. (Fig.3)
|
|
Paso 3
A B C D E F G H I J K L M
0 0 0 5 7 6 0 1 8 5 1 8 4
+ 5 6 Paso 3
0 0 0 5 7 6 0 1 8"10"7 8 4
|
| * Puede ser interesante notar que muchos Soroban japoneses fabricados entre alrededor de 1850 y 1930 tienen una cuenta del cielo y cinco cuentas de la tierra. (es decir, 1 cuenta por encima de la barra central y 5 cuentas por debajo). Siempre me ha intrigado por qué podría ser esto. Aprender de algunas de estas técnicas más antiguas puede proporcionar una pista. En el paso 3 se podría, como alternativa, mostrar el número 10 en la barra J como una cuenta del cielo hacia abajo y 5 cuentas de la tierra hacia arriba.* |
3a: A partir de aquí podemos continuar. Multiplicamos el 8 en la columna I bpor el 6 en F y sumamos el producto 48 en KL
3b: Multiplicamos el 8 en la columna I por el 5 en D, quitamos el 8 en I y sumamos el producto 40 en las columnas IJ. Esto nos deja 1 4 "11" 2 6 4 en las columnas H - M.
3c: A continuación quitamos el 10 de la varilla J y lo llevamos a la columna I cambiando el 4 a 5. Esto nos deja 151264 en las columnas H - M. (Fig.4)
|
|
Steps 3a-3b-3c
A B C D E F G H I J K L M
0 0 0 5 7 6 0 1 8"10"7 8 4
+ 4 8 Paso 3a
+ (4)0 Paso 3b
0 0 0 5 7 6 0 1 4"11"2 6 4
+ cuenta extra 1 0 Paso 3c
0 0 0 5 7 6 0 1 5 1 2 6 4
|
Paso 4: Ahora podemos continuar normalmente usando complementos. Multiplicamos el 1 en la varilla H por el 7 en E y sumamos el producto 7 en la columna J
4a: Multiplicamos el 1 en la varilla H por el 6 en F y sumamos el producto 6 en la columna K
4b y resultado: Multiplicamos el mismo 1 en la varilla H por el 5 en D, quitamos el 1 de la columna H y sumamos el producto 5. Esto nos deja 108,864 en las columnas H - M, lo cual constituye el resultado. (Fig.5)
|
|
Paso 4
A B C D E F G H I J K L M
0 0 0 5 7 6 0 1 5 1 2 6 4
+ 0 7 Paso 4
+ 0 6 Paso 4a
+ 0 5 Paso 4b
0 0 0 5 7 6 0 1 0 8 8 6 4
|
Ejemplo 4: "La Cuenta Suspendida" (Xuan - zhu)
En el siguiente ejemplo, usaremos una técnica en la que bajamos la segunda cuenta superior hasta la mitad de la varilla para que no toque ni el marco de arriba ni la cuenta de abajo. Esta cuenta suspendida tiene un valor de 10. Una vez más, al resolver el siguiente ejemplo, usaremos números complementarios tanto como sea posible. Sin embargo, en dos casos quedará claro que tener cuentas adicionales simplifica el proceso.
Es de destacar que, si bien es divertido hacer un problema como este, es un ejemplo bastante extremo y los casos en los que se necesita la cuenta suspendida son bastante raros.
989 x 898 = 888, 122
Paso 1: Situamos el multiplicador 898 en DEF y el multiplicando 989 en HIJ. (Fig.6)
|
|
Paso 1
A B C D E F G H I J K L M
0 0 0 8 9 8 0 9 8 9 0 0 0
|
Paso 2: Multiplicamos el 9 en la columna J por el 9 en E y sumamos el producto 81 en KL.
2a: Multiplicamos el 9 en la columna J por el 8 en F y sumamos el producto 72 en LM
2b: Multiplicamos el mismo 9 en la columna J por el 8 en la varilla D, quitamos el 9 de J y sumamos el producto 72 en JK . Esto deja 988082 en las columnas H - M. (Fig.7)
|
|
Paso 2
A B C D E F G H I J K L M
0 0 0 8 9 8 0 9 8 9 0 0 0
+ 8 1 Paso 2
+ 7 2 Paso 2a
(7)2 Paso 2b
0 0 0 8 9 8 0 9 8 8 0 8 2
|
Aquí es donde usamos la Cuenta suspendida. En este punto, vamos
a multiplicar el 8 en la barra I por el 9 en E. Si tuviéramos que hacer
un acarreo aquí, tendríamos que cambiar el 8 por 9. Eso sería confuso.
(Especialmente porque es el 8 el que se va a multiplicar por cada uno de los
dígitos del multiplicador). Podríamos despistarnos. En lugar de ello, utilizaremos
la técnica de "Cuenta suspendida".
Paso 3: Multiplicamos el 8 de la columna I por el 9 en E y sumamos el producto 72 en JK. Al bajar la cuenta suspendida para representar 10 y restado 3 hemos sumado 7 a la barra J dando a esta barra un valor total de 15.
3a: Multiplicamos el 8 de la columna I por el 8 en F y sumamos el producto 64 en KL. Esto deja un valor de 9 8 "15" 9 2 2 en las columnas H - M. (Fig.8)
|
|
Paso 3-3a
A B C D E F G H I J K L M
0 0 0 8 9 8 0 9 8 8 0 8 2
+ 7 2 Paso 3
+ 6 4 Paso 3a
0 0 0 8 9 8 0 9 8"15"9 2 2
|
3b: Multiplicamos el mismo 8 de la columna I por el 8 en la columna D, quitamos el 8 de I y sumamos el producto 64 en IJ . Esto deja 9 6 "19" 9 2 2 en las columnas H - M.
3c: A continuación quitamos el 10 "Suspendido" de la columna J y lo llevamos a la columna I cambiándola de 6 a 7. Esto deja 979922 en las varillas H - M. (Fig.9)
|
|
Paso 3b-3c
A B C D E F G H I J K L M
0 0 0 8 9 8 0 9 8"15"9 2 2
(6)4 Paso 3b
0 0 0 8 9 8 0 9 6"19"9 2 2
+ suspendida 1 0 Paso 3c
0 0 0 8 9 8 0 9 7 9 9 2 2
|
Paso 4: Multiplicamos el 9 en H por el 9 en E y sumamos el producto 81 en IJ usando la técnica de la Cuenta Suspenddida.
4a: Multiplicamos el 9 en H por el 8 en F y sumamos el producto 72 en JK. Esto deja 9 "16" 8 1 2 2 en HIJKLM. (Fig.10)
|
|
Steps 4-4a
A B C D E F G H I J K L M
0 0 0 8 9 8 0 9 7 9 9 2 2
+ 8 1 Paso 4
+ 7 2 Paso 4a
0 0 0 8 9 8 0 9"16"8 1 2 2
|
4b: Multiplicamos el 9 en H por el 8 en D, quitamos el 9 de H y sumamos el producto 72 en HI. Esto deja 7 "18" 8 1 2 2 en las columnas H - M.
4c y resultado: A continuación quitamos el 10 "Suspendido" de la varilla I y lo llevamos a la columna H cambiando el 7 en 8. Esto deja 888122 en las varillas H - M, como resultado. (Fig.11)
|
|
Paso 4b-4c
A B C D E F G H I J K L M
0 0 0 8 9 8 0 9"16"8 1 2 2
(7)2 Paso 4b
0 0 0 8 9 8 0 7"18"1 2 2
+ suspendido 1 0 Paso 4c
0 0 0 8 9 8 0 8 8 8 1 2 2
|
A lo largo de los siglos, tanto los japoneses como los chinos han desarrollado
y utilizado muchas técnicas diferentes para resolver problemas de multiplicación
en el ábaco. Uno ampliamente utilizado es
el ilustrado en el libro de 1954:
"The Japanese Abacus, its use and Theory" de Takashi Kojima. Al presentar
su técnica, incluso Kojima dice: "Hay varios métodos de multiplicación con el
ábaco. El que se presenta en las siguientes páginas es un método reciente..."
Aunque es posible resolver problemas de multiplicación usando estas técnicas chinas en un Soroban de 1/4 cuentas, los ejemplos anteriores muestran que los resultados se obtienen más fácilmente con la ayuda de cuentas adicionales.
Artículo traducido del
original
en lengua inglesa
por Jesús Cabrera - gmail: jccsvq
(2022)
▪ Abacus: Mystery of the Bead
▪ Técnicas Avanzadas para el Ábaco
Junio de 2004
Totton Heffelfinger Toronto Ontario Canada
Email
totton[at]idirect[dot]com
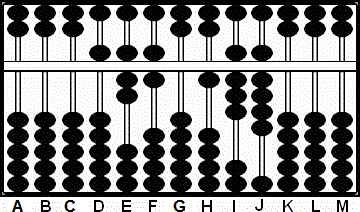 Fig. 1
Fig. 1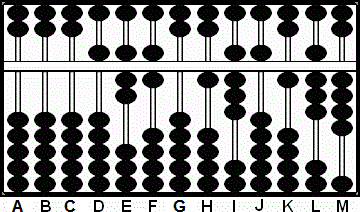 Fig. 2
Fig. 2 Fig. 3
Fig. 3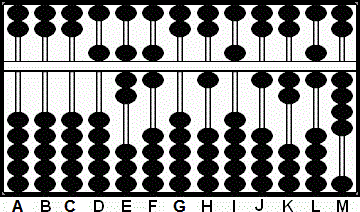 Fig. 4
Fig. 4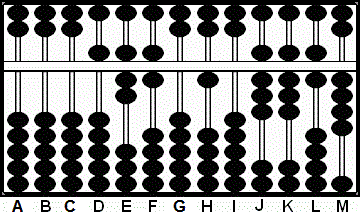 Fig. 5
Fig. 5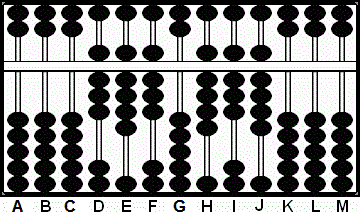 Fig. 6
Fig. 6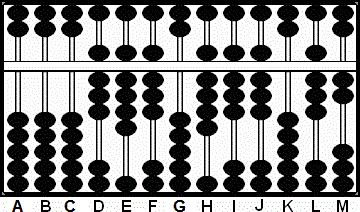 Fig. 7
Fig. 7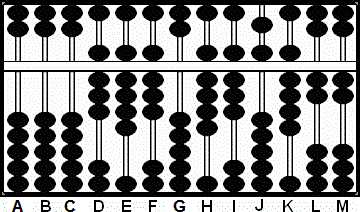 Fig. 8
Fig. 8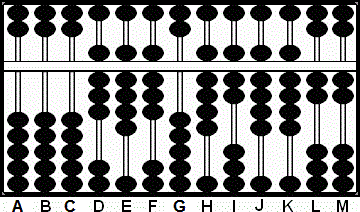 Fig. 9
Fig. 9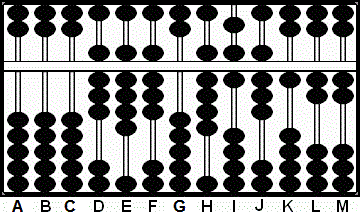 Fig. 10
Fig. 10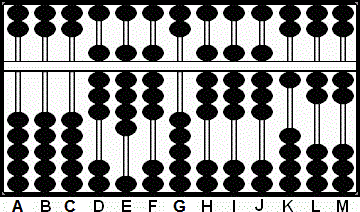 Fig. 11
Fig. 11