ABACUS: MYSTERY OF THE BEAD
The Bead Unbaffled - An Abacus Manual
 RAÍCES CUADRADAS
RAÍCES CUADRADAS
Este tutorial se remonta a octubre de 2003 cuando lo escribí como un capítulo para el Manual Soroban/Abacus de Dave Bernazzani. Lo recreo aquí ya que las páginas de Dave han estado fuera de línea a partir de mayo de 2006. - T.P.H
Cuando se trata de extraer raíces cuadradas, es cierto, no puedo recordar la última vez que necesité extraer la raíz cuadrada de un número grande y aplicarla a algo práctico. Supongo que yo sólo quería aprender esta técnica porque me resultaba increíble que se pudiera hacer con un ábaco. De hecho no sólo puede hacerse, sino que usar un ábaco lo facilita.
Existen diferentes técnicas que se pueden utilizar para extraer raíces cuadradas utilizando un ábaco. Usaré la que Takashi Kojima parece preferir en su libro Advanced Abacus - Theory and Practice. En lugar de confundirnos con un montón de fórmulas algebraicas, nos limitaremos a ver cómo se hace en el ábaco. Para mí esto lo hace más interesante y, ciertamente, me lo hace menos confuso porque de todos modos no entiendo las fórmulas algebraicas.
Para ilustrar la técnica, usaré los términos número cuadrado, número raíz y cuadrado. El número cuadrado se refiere al número del que se va a extraer la raíz cuadrada y siempre se coloca en el lado derecho del ábaco. El número raíz se refiere al número que eventualmente forma nuestra respuesta y siempre se coloca en el lado izquierdo del ábaco. Elevar un número al cuadrado se refiere a multiplicar un número por sí mismo como en el ejemplo, 3 x 3 = 9.
Al prepararse para encontrar la raíz cuadrada de un número, ya sea en el papel o en el ábaco, el número normalmente se separa en pares de dígitos. En el ejemplo 17,362.236 comenzando en el punto decimal y moviéndose hacia la izquierda y hacia la derecha, los números se separarían 1' 73' 62'. 23' 60. Debido a las limitaciones de usar un pequeño ábaco de pocos dígitos, haremos la separación y emparejamiento mentalmente. Kojima hace lo mismo en su libro.
Aunque la técnica involucra solo matemáticas simples y, por lo tanto, es bastante fácil de realizar, el proceso de extracción es un tanto complicado y laborioso. Por esta razón, tratar de explicar cómo funciona todo puede ser un ejercicio de confusión y quizás fuera mejor saltárselo y aprender de los ejemplos que siguen; sin embargo, a modo de breve explicación:
- Comenzamos colocando el número del que se va a extraer la raíz cuadrada en el lado derecho del ábaco. Este número a la derecha es el "número cuadrado".
- Dividimos el número cuadrado en pares como se describe arriba.
- Miramos el primer grupo de números emparejados (puede ser un único número) y determinamos el cuadrado perfecto más grande que es menor o igual que el grupo. Restamos ese cuadrado perfecto del grupo.
- Tomamos la raíz cuadrada de dicho cuadrado perfecto y la colocamos en el lado izquierdo del ábaco. Este número de la izquierda es el "número raíz" y eventualmente formará nuestra respuesta.
- Duplicamos el número raíz y dividimos por él el siguiente grupo del número cuadrado de la derecha. Colocamos el cociente junto al primer número raíz.
- Mentalmente elevamos al cuadrado dicho cociente y lo restamos del número cuadrado de la derecha.
- Continamos el proceso hasta que se agote el número cuadrado de la derecha. En caso de que el número cuadrado no sea un cuadrado perfecto, se pueden agregar más grupos de 00 y continuar el proceso para obtener decimales.
- Cuando hayamos terminado, reduciremos a la mitad el número raíz de la izquierda. Lo que quede será el resultado de la raíz cuadrada.
¿Confundido? Creo que sí, pero anímese, seguir los siguientes ejemplos en su ábaco debería aclararle las cosas.
Ejemplo 1. \/ 1156 = ?
Paso 1: Colocamos 1156 en el lado derecho del ábaco. Este es el número cuadrado. Si hay espacio, empareje 11 56 o lo hacemos mentalmente. Debido a que hay dos grupos (11 y 56), el resultado tendrá dos dígitos posiblemente seguidos de una fracción decimal. (Fig. 1)
|
Paso 1
A B C D E F G H I J K L M
. . . .
0 0 0 0 0 1 1 5 6 0 0 0 0
|
Paso 2: Ahora miramos el primer grupo de números. (En este caso, el 11 en las varillas F y G). Buscamos el cuadrado perfecto más grande que sea menor o igual a 11. La respuesta es 9. Restamos 9 de 11 dejando 2. Ponemos la raíz cuadrada de 9 (es decir, 3) en algún lugar en el lado izquierdo del ábaco, en este caso en la varilla B. Esto forma la primera parte de la raíz del número. (Fig.2)
|
Paso 2
A B C D E F G H I J K L M
. . . .
0 3 0 0 0 1 1 5 6 0 0 0 0
- 9
0 3 0 0 0 0 2 5 6 0 0 0 0
|
Paso 3: Duplicamos el 3 en la varilla B dando 6 y dividimos 25 en las varillas G y H por 6. 6 cabe en 25 cuatro veces con un resto. Colocamos 4 en la varilla C. Multiplicamos 6 x 4 dando 24 y restamos este 24 de 25. Eso deja 16 en las varillas H e I. (Fig. 3)
|
Paso 3
A B C D E F G H I J K L M
. . . .
0 6 0 0 0 0 2 5 6 0 0 0 0
4
-2 4
0 6 4 0 0 0 0 1 6 0 0 0 0
|
Paso 4: Ahora elevamos mentalmente al cuadrado el 4 de la barra C y restamos el producto del resto de la derecha. 4 x 4 = 16. Perfecto. Restamos 16 de las barras H e I. (Fig.4)
|
Paso 4
A B C D E F G H I J K L M
. . . .
0 6 4 0 0 0 0 1 6 0 0 0 0
(4)
- 1 6
0 6 4 0 0 0 0 0 0 0 0 0 0
|
Paso 5: Ya casi está. En el Paso 3 doblamos el 3 de la varilla B dando 6. Ahora hay que reducirlo a la mitad, al 3 original y tendremos la respuesta al problema en las varillas B y C. (Fig.5)
El resultado 34 en las varillas B y C.
|
____ \/ 1156 = 34 |
* He incluido el siguiente ejemplo porque ilustra dónde es posible confundirse un poco y tomar un camino equivocado. Si bien el problema se supera fácilmente, es algo a tener en cuenta.
Ejemplo 2. \/ 74,529 = ?
Paso 1: Colocamos 74,529 en el lado derecho del ábaco. Este es el número cuadrado. Si hay espacio, empareje 7 45 29 o hágalo mentalmente. **Observe el emparejamiento extraño. El número 7 está solo y se considerará el primer grupo.** Debido a que hay tres grupos (7, 45 y 29), sabemos que la respuesta tendrá tres números enteros posiblemente seguidos de una fracción decimal. (Fig.6)
|
Paso 1
A B C D E F G H I J K L M
. . . .
0 0 0 0 0 0 0 7 4 5 2 9 0
|
Paso 2: Nos fijamos en el primer grupo de números. (En este caso, solo hay 7 en la barra H). Buscamos el cuadrado perfecto más grande que sea menor o igual a 7. La respuesta es 4. Restamos 4 de 7 dejando 3. Ponemos la raíz cuadrada de 4 (es decir, 2) en algún lugar en el lado izquierdo del ábaco, en este caso en la varilla D. Esto forma la primera parte del número raíz. (Fig.7)
|
Paso 2
A B C D E F G H I J K L M
. . . .
0 0 0 2 0 0 0 7 4 5 2 9 0
- 4
0 0 0 2 0 0 0 3 4 5 2 9 0
|
Paso 3: Ahora doblamos el 2 en la varilla D dando 4 y dividimos 34, en las varillas G y H , entre 4. Normalmente tendríamos que 34 ÷ 4 = 8 con un resto. Pero....
|
* Aquí es donde la cosa se pone interesante. La técnica requiere que después de dividir 34 entre 4 hay que restar el cuadrado del cociente. En otras palabras, tiene que quedar suficiente en el resto. ¿Lo ve? Si elegimos 34 ÷ 4 = 8, solo quedará 25 en las varillas I y J. Eso no es suficiente para restar 8 x 8 = 64. Sin embargo, si elegimos 34 ÷ 4 = 7, quedará 65 en las varillas. I y J. Y 65 deja suficiente para restar el cuadrado 7 x 7 = 49. ¿Ve lo que quiero decir? Aunque 8 sea la respuesta correcta al problema de división, no podemos usar 8 porque no podemos restar su cuadrado. Tenemos que conformarnos con 7. Si bien este tipo de problema no siempre surge, es algo que puede suceder. |
Bien, es 7. 4 cabe en 34 siete veces con resto. Colocamos 7 en la barra E. Multiplicamos 4 x 7, dando 28, y restamos 28 de 34 en las barras H e I. Con 65 como resto en I y J, hay suficiente para trabajar el Paso 4. (Fig.8)
|
Paso 3
A B C D E F G H I J K L M
. . . .
0 0 0 4 0 0 0 3 4 5 2 9 0
7
- 2 8
0 0 0 4 7 0 0 0 6 5 2 9 0
|
Paso 4: Ahora que nos hemos asegurado de que queda suficiente para trabajar, tomamos el 7 en la varilla E y restamos su cuadrado del resto de la derecha. 7 x 7 = 49. Restamos 49 de 65 en las varillas I y J dejando 16. (Fig.9)
|
Paso 4
A B C D E F G H I J K L M
. . . .
0 0 0 4 7 0 0 0 6 5 2 9 0
(7)
- 4 9
0 0 0 4 7 0 0 0 1 6 2 9 0
|
Paso 5: Ahora duplicamos el 7 en la varilla E dando 14. Colocamos 14 en las varillas E y F. (Fig.10)
|
Paso 5
A B C D E F G H I J K L M
. . . .
0 0 0 4 7 0 0 0 1 6 2 9 0
+ 7
0 0 0 4 1 4 0 0 1 6 2 9 0
|
Paso 6: Ahora dividimos el 1629 de la derecha por el 414 de las barras D, E y F. Parece que 414 entra en 1629 tres veces con un resto. Colocamos 3 en la barra G y lo multiplicamos por el 4 de la barra D dando 12. Restamos este 12 de 16 en las barras I y J. Nos queda 4.
Paso 6(a): Ahora multiplicamos 3 por el 1 de la barra E dando 3 y restamos 3 de la barra J.
Paso 6(b): A continuación multiplicamos 3 por el 4 de la barra F dando 12 y restamos 12 de las barras J y K. (Fig.11)
Resultado tras los pasos 6, 6(a) y 6(b)
|
Pasos 6, 6(a), 6(b)
A B C D E F G H I J K L M
. . . .
0 0 0 4 1 4 0 0 1 6 2 9 0
3
- 1 2
0 0 0 4 1 4 3 0 0 4 2 9 0
- 3
0 0 0 4 1 4 3 0 0 1 2 9 0
-1 2
0 0 0 4 1 4 3 0 0 0 0 9 0
|
Paso 7: El resto es fácil. Todo lo que queda por hacer en este paso es elevar al cuadrado mentalmente el 3 y restar el resultado del resto de la derecha. 3 x 3 = 9. Restamos 9 de la varilla L. (Fig.12)
|
Paso 7
A B C D E F G H I J K L M
. . . .
0 0 0 4 1 4 3 0 0 0 0 9 0
(3)
- 9
0 0 0 4 1 4 3 0 0 0 0 0 0
|
Paso 8: Casi terminado. En los pasos 3 y 5 duplicamos porciones del número raíz. Ahora deben reducirse a la mitad, a sus números originales. Tomamos la mitad de 4 en la barra D dando 2. Tomamos la mitad de 14 en las barras E y F dando 7 y lo colocamos en la barra E. Movemos el 3 en G a la barra F. Y ahí está la respuesta. (Fig.13)
Resultado final 273 en las varillas D, E y F.
|
_____ \/ 74529 = 273 |
Ejemplo 3. \/ 39.3129 = ?
Paso 1: Este ejemplo implica un número decimal. Colocamos 39.3129 en el lado derecho del ábaco. Este es el número cuadrado. Si hay espacio, emparejamos 39. 31 29, si no lo hacemos mentalmente. El primer grupo es el número entero 39 en las varillas H e I. Por esto sabemos que la respuesta tendrá un dígito entero. Todo lo que sigua será una fracción decimal. (Fig.14)
|
Paso 1
A B C D E F G H I J K L M
. . . .
0 0 0 0 0 0 0 3 9 3 1 2 9
|
Paso 2: Ahora miramos el primer grupo de números. (En este caso, el 39 en las varillas H e I). Buscamos el cuadrado perfecto más grande que sea menor o igual a 39. La respuesta es 36. Restamos 36 de 39 dejando 3. Ponemos la raíz cuadrada de 36 (es decir, 6) en algún lugar en el lado izquierdo del ábaco, en este caso en la varilla C. Esto forma la primera parte del del número raíz. (Fig.15)
|
Paso 2
A B C D E F G H I J K L M
. . . .
0 0 6 0 0 0 0 3 9 3 1 2 9
- 3 6
0 0 6 0 0 0 0 0 3 3 1 2 9
|
Paso 3: Doblamos el 6 en la varilla C dando 12 y colocamos 12 en las varillas B y C. (Fig.16)
|
Paso 3
A B C D E F G H I J K L M
. . . .
0 0 6 0 0 0 0 0 3 3 1 2 9
+ 6
0 1 2 0 0 0 0 0 3 3 1 2 9
|
Paso 4: Dividimos 33 en las barras I y J entre 12. 12 cabe en 33 dos veces dejando un resto. Colocamos 2 en la barra D. Multiplicamos 12 x 2 dando 24 y restamos 24 de 33. Eso deja 9 en la barra J. (Fig.17)
|
Paso 4
A B C D E F G H I J K L M
. . . .
0 1 2 0 0 0 0 0 3 3 1 2 9
2
- 2 4
0 1 2 2 0 0 0 0 0 9 1 2 9
|
Paso 5: Mentalmente elevamos el 2 en la barra D al cuadrado y lo restamos del resto a la derecha. 2 x 2 = 4. Restamos 4 de la varilla K. (Fig.18)
|
Paso 5
A B C D E F G H I J K L M
. . . .
0 1 2 2 0 0 0 0 0 9 1 2 9
(2)
- 4
0 1 2 2 0 0 0 0 0 8 7 2 9
|
Paso 6: Duplicamos el 2 en la barra D dando 4 y dejando 124 en las barras B, C y D.. (Fig.19)
|
Paso 6
A B C D E F G H I J K L M
. . . .
0 1 2 2 0 0 0 0 0 9 1 2 9
+ 2
0 1 2 4 0 0 0 0 0 8 7 2 9
|
Paso 7: Ahora dividimos el 8729 de la derecha por el 124 de las varillas B, C y D. Parece que 124 cabe en 8729 siete veces dejando un resto. Colocamos 7 en la barra E y lo multiplicamos por el 1 en la barra B dando 7. Restamos 7 de 8 en la barra J dejando 1.
Paso 7(a): Multiplicamos el 7 por el 2 en la barra C dando 14. Restamos 14 de las barras J y K.
Paso 7(b): Multiplicamos 7 por 4 en la barra D dando 28. Restamos 28 de las barras K y L. (Fig.20)
Resultado tras los pasos 7, 7(a) and 7(b)
|
Pasoss 7, 7(a), 7(b)
A B C D E F G H I J K L M
. . . .
0 1 2 4 0 0 0 0 0 8 7 2 9
7
- 7
0 1 2 4 7 0 0 0 0 1 7 2 9
- 1 4
0 1 2 4 7 0 0 0 0 0 3 2 9
- 2 8
0 1 2 4 7 0 0 0 0 0 0 4 9
|
Paso 8: Casi estamos. Mentalmente elevamos al cuadrado el 7 de la barra E y los restamos del resto a la derecha. 7 x 7 = 49. Restamos 49 de las barras L y M. (Fig.21)
|
Paso 8
A B C D E F G H I J K L M
. . . .
0 1 2 4 7 0 0 0 0 0 0 4 9
(7)
- 4 9
0 1 2 4 7 0 0 0 0 0 0 0 0
|
Paso 9: El último paso. En los pasos 3 y 6 duplicamos porciones del número raíz. Ahora deben reducirse a la mitad, a sus números originales. Tomamos la mitad de 12 en las varillas B y C dando 6. Colocamos 6 en la varilla C. Tomamos la mitad de 4 en la varilla D dando 2. Ya tenemos la respuesta. (Fig.22)
Resultado 6.27 en las columnas C, D y E.
|
_______ \/ 39.3129 = 6.27 |
Artículo traducido del original en lengua inglesa
por Jesús Cabrera - gmail: jccsvq
(2022)
▪
Abacus: Mystery of the Bead
▪
Técnicas Avanzadas para el Ábaco
© Octubre de 2003
Totton Heffelfinger
Toronto Ontario Canada
Email
totton[at]idirect[dot]com
 Fig.1
Fig.1 Fig. 2
Fig. 2 Fig. 3
Fig. 3 Fig.4
Fig.4 Fig. 5
Fig. 5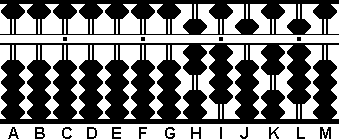 Fig. 6
Fig. 6 Fig. 7
Fig. 7 Fig. 8
Fig. 8 Fig. 9
Fig. 9 Fig.10
Fig.10 Fig.11
Fig.11 Fig.12
Fig.12 Fig.13
Fig.13 Fig.14
Fig.14 Fig.15
Fig.15 Fig.16
Fig.16 Fig.17
Fig.17 Fig.18
Fig.18 Fig.19
Fig.19 Fig.20
Fig.20 Fig.21
Fig.21 Fig.22
Fig.22