ABACUS: MYSTERY OF THE BEAD
The Bead Unbaffled - An Abacus Manual
 Encontrar el MCD y el MCM
de dos números
Encontrar el MCD y el MCM
de dos números
** Antes de comenzar con estas técnicas es importante comprender el uso básico del Soroban japonés **
MCD: El máximo común divisor de dos números es el mayor número entero que puede dividir exactamente a ambos números. (Nota: Si el MCD de dos números es 1, ambos números se dicen primos entre sí, primos relativos o coprimos.)
El MCD de 12 y 18
Los factores primos de 12 son: 2 x 2 x
3
Los factores primos de 18 son: 2 x
3 x 3
Los factores primos en común de 12 y 18 son 2 y 3
El máximo común divisor de 12 y 18 es 6
LCM: El mínimo común múltiplo de dos números es el menor entero (distinto de cero) que es múltiplo de ambos números.
El MCM de 12 y 18
Los múltiplos de 12 son: 0, 12, 24, 36, 48, 60,
72...
Los múltiplos de 18 son: 0, 18, 36, 54,
72, 90, 108...
Tanto 12 como 18 comparten los múltiplos 36, 72
y ...
Pero el múltiplo más pequeño compartido por ambos es
36
Afortunadamente existe una manera muy simple y eficiente de encontrar el MCD y el MCM para dos números. Las siguientes técnicas de soroban me fueron mostradas por Enriello y por Edvaldo Siqueira, ambos miembros del grupo de noticias Soroban / Abacus. Para encontrar el MCD y el MCM de dos números (a, b) las técnicas funcionan así:
- Coloque los dos números (a, b) en el lado izquierdo de soroban.
- Coloque el primer número (a) una vez más a la derecha.
- Trabajando en la derecha, multiplique a*b y agregue el producto al marco.
- Usando el algoritmo de Euclides*, encuentre el MCD de a y b a la izquierda.
- Use el producto calculado en el paso 3 para encontrar el MCM. MCM = a*b / MCD.
* El algoritmo de Euclides se realiza fácilmente en un ábaco. Comience restando el número más pequeño del mayor tantas veces como sea posible. En caso de que quede un resto, invierta el proceso y reste el nuevo número más pequeño del más grande. Este proceso se continúa de un lado a otro hasta que sólo quede un número. Ese número restante es el MCD. (Nota: si en algún momento los números son radicalmente diferentes en tamaño, en lugar de restar, la división puede ser mejor opción).
Example 1: Find the GCD and LCM for 12 & 18
Paso 1: Entre 12 en las columnas AB y 18 en DE. Ponga otro 12 en JK. (Fig.1)
|
|
Paso 1
A B C D E F G H I J K L M N O
. . . . .
1 2 0 1 8 0 0 0 0 1 2 0 0 0 0
|
Paso 2: Multiplique el 12 en las columnas JK por el 18 en DE. Sume el producto 216 a las varillas LMN. (Fig.2)
|
|
Paso 2 A B C D E F G H I J K L M N O
. . . . .
1 2 0 1 8 0 0 0 0 0 0 2 1 6 0
|
Encontrar el MCD de 12 y 18 usando el algoritmo de Euclides
Paso 3: Restar 12 de 18 en las columnas DE. El resultado es 6. (Fig.3)
|
|
Paso 3 A B C D E F G H I J K L M N O
. . . . .
1 2 0 0 6 0 0 0 0 0 0 2 1 6 0
|
Paso 4 y el MCD: Damos la vuelta al proceso y restamos 6 del 12 en las columnas AB.
Esto puede hacerse dos veces quedando cero. Como no puede haber más sustracciones,
concluimos que el máximo común divisor para este problema es 6 en la columna E. (Fig.4)
|
|
Paso 4 A B C D E F G H I J K L M N O
. . . . .
0 0 0 0 6 0 0 0 0 0 0 2 1 6 0
|
Ahora calculamos el MCM dividiendo el 216 de las columnas LMN por el 6 de la columna E.
Paso 5 y MCM: Dividimod el 216 de las varillas LMN por el 6 en E. Con este último paso conoceremos que el mínimo común múltiplo de 12 y 18 es el cociente 36 encontrado en las varillas KL. (Fig.5)
|
|
Paso 5 A B C D E F G H I J K L M N O . . . . . 0 0 0 0 6 0 0 0 0 0 3 6 0 0 0 .<- * * Kojima Enseña: desplaza la columna unidad tantas posiciones a la izquierda como cifras enteras tiene el divisor +1. |
Resultado: MCD de 12 y 18 = 6 : MCM de
12
y 18 = 36
Ejemplo 2: Encontrar el MCD y MCM de 39 y 91
Paso 1: Entre 39 en las columnas AB y 91 en DE. Entre otro 39 en JK. (Fig.6)
|
|
Paso 1
A B C D E F G H I J K L M N O
. . . . .
3 9 0 9 1 0 0 0 0 3 9 0 0 0 0
|
Paso 2: Multiplique 39 en las columnas JK por 91 en DE. Sume el producto 3549 a
las varillas KLMN. (Fig.7)
|
|
Paso 2 A B C D E F G H I J K L M N O
. . . . .
3 9 0 9 1 0 0 0 0 0 3 5 4 9 0
|
Encontrar el MCD de 39 y 91 usando el algoritmo de Euclides
Paso 3: Restar 39 de 91 en las columnas DE. Esto puede hacerse dos veces quedando 13. (Fig.8)
|
|
Paso 3 A B C D E F G H I J K L M N O
. . . . .
3 9 0 1 3 0 0 0 0 0 3 5 4 9 0
|
Paso 4 y el MCD: Damos la vuelta al proceso y restamos 13 de 39 en AB. Esto
puede hacerse tres veces quedando cero. Puesto que no puede haber más sustracciones,
sabemos que el máximo común divisor de este problema es 13 en las columnas DE. (Fig.4)
|
|
Paso 4 A B C D E F G H I J K L M N O
. . . . .
0 0 0 1 3 0 0 0 0 0 3 5 4 9 0
|
Ahora obtenemos el MCM dividiendo 3549 en las columnas KLMN por 13 en DE.
Paso 5 y MCM: Dividimos 3549 en las columnas KLMN por 13 en DE. Con este último paso conocemos que el mínimo común múltiplo de 39 y 91 es el cociente 273 en las columnas IJK. (Fig.5)
|
|
Paso 5 A B C D E F G H I J K L M N O . . . . . 0 0 0 1 3 0 0 0 2 7 3 0 0 0 0 .<- - * * Kojima teaches; move the decimal 1 place + 1 to the left for every whole number in a divisor. |
Resultado: MCD de 39 y 91 = 13 : MCM de 39 y 91 = 273
Compruebe sus resultados con las calculadoras de MCD and MCM
LCM @ math
is fun
&
GCD @ math
is fun
|
REFERENCIAS: Wikipedia
Kojima,
Takashi. Tani, Yukio
Edvaldo Siquiera
Miembros del grupo de noticias Soroban / Abacus |
▪
Abacus: Mystery of the Bead Página Imprimible (formato pdf )
|
Artículo traducido del original
en lengua inglesa
por Jesús Cabrera - gmail: jccsvq
(2022)
© Abril de 2006
Totton Heffelfinger Toronto Ontario Canada
Email
totton[at]idirect[dot]com
 Fig. 1
Fig. 1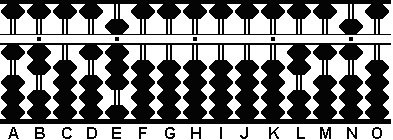 Fig. 2
Fig. 2 Fig. 3
Fig. 3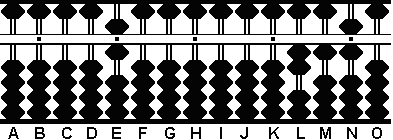 Fig. 4
Fig. 4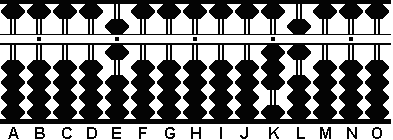 Fig. 5
Fig. 5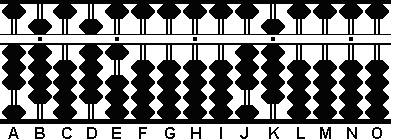 Fig. 6
Fig. 6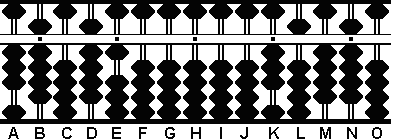 Fig. 7
Fig. 7 Fig. 8
Fig. 8 Fig. 9
Fig. 9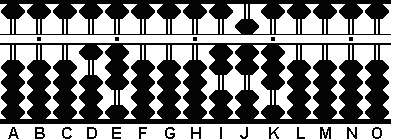 Fig. 10
Fig. 10