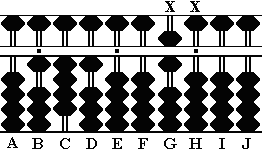ABACUS: MYSTERY OF THE BEAD
The Bead Unbaffled - An Abacus Manual
![]() FIND THE SQUARE ROOT OF 2 TO SEVEN DECIMAL
PLACES
FIND THE SQUARE ROOT OF 2 TO SEVEN DECIMAL
PLACES
I've often wished that Professor Kato had gone a little further and illustrated his technique using one or two examples where he would take a large decimal answer from a whole number. Here's a Square Root problem that's a good example. Because of its long decimal answer, we get a pretty good feel for the technique and for how numbers should be placed on the soroban.
Kato's methods for finding the
Square Root of a number have been well documented. Please study them first. With the exception of the first few
steps, this example will only show images of the soroban after completing each of the operations. The diagrams
can be used as a guideline to help assess one's understanding of the technique.
A Couple of things to Remember:
i) In the following it's important to remember that where possible the numbers making up the radicand are always divided into groups of two. When finding the Square Root of 2 the first group is 02. Subsequent groups are paired as 00 00 00 and so on.
ii) Prof. Kato shows us how to subtract 1/2 of a squared number (main page). As a result, sometimes fractions like 0.5, 4.5, 12.5, etc. will come into play. Remember, because it's a fraction, when subtracting 0.5 the operation will always carry another 0.5 over into the next pairing of numbers (see steps 1b and 3b for clarification).
To illustrate I'll do the first few steps of finding the square root of 2.
In this step the group is 02 on rod CD with the next pair 00
(XX) on rods EF.
|
Step 1: Find the square root of 2. Set 2 on rod D. The group at this point is 02 on rod CD and the pair 00 on rods EF. (Fig. A) |
Fig. A |
|
|
Step 1a: Find the largest perfect square that is less than or equal to 2. The answer is 1. Place 1 on rod. B Square 1 on B (1 x 1 = 1), subtract 1 from 2 on rod D leaving 1. (Fig. B) |
Fig. B |
|
|
Step 1b: Subtract *half* of 1 from rod D. This carries 0.5 over to Rod E in the next pairing. (Fig. C)
|
Fig. C |
|
In each of the division steps below there must be enough remainder
to subtract *half* the answer squared. Watch this next step.
|
Step 2: Divide 1 on rod B into 5 on rod E. It looks like the answer should be 5, but the technique requires a remainder. Choose 4 instead. The resulting remainder allows us to complete Step 2a (see below). Place the answer 4 on rod C. Multiply 4 on C by 1 on B and subtract the result from 5 on rod E. This leaves 1. (Fig. D)
|
Fig. D |
|
|
Step 2a: Square 4 on rod C (4 x 4 = 16) and subtract *half* (8) from rods EF. This leaves the partial answer 1.4 on rods BC and a remainder 2 on rod F. (Fig. E) |
Fig. E |
|
In this step add another pairing of 00 (XX), this time to rods GH.
|
Step 3: Divide 1 on B into 2 on F and place the answer 1 on rod D. Multiply 1 on rod D by 1 on B (1 x 1 = 1). Subtract 1 from 2 on Rod F leaving 1. (Fig. F) |
Fig. F |
|
|
Step 3a: Multiply 1 on rod D by 4 on C (1 x 4 = 4). Subtract 4 from rods FG. This leaves 6 on rod G. (Fig. G)
|
Fig. G |
|
|
Step 3b: Square 1 on rod D (1 x 1 = 1) and subtract *half* (0.5) from the remainder. This leaves the partial answer 1.41 on rods BCD and the remainder 595 on rods GHI. (Fig. H) **When subtracting 0.5 (not a whole number) from rod H it adds 0.5 to the next pairing of numbers, in this case rod I. ** |
Fig. H |
|
In this step add another pairing of 00 (XX), this time to rods IJ.
|
Step 4: Divide 1 on rod B into 5 on rod G. Place the answer 4 on rod E. Multiply 4 on E by 1 on B and subtract the result from rod G. (Fig. I) |
Fig. I |
|
|
Step 4a: Multiply 4 on E by 4 on C and subtract 16 from rods GH. (Fig. J)
|
Fig. J |
|
|
Step 4b: Multiply 4 on E by 1 on D and subtract 04 from rods HI. (Fig. K)
|
Fig. K |
|
|
Step 4c: Square 4 on rod E (4 x 4 = 16) and subtract *half* (8) from rods IJ. This leaves the partial answer 1.414 on rods BCDE and the remainder 302 on rods JIJ. (Fig. L) |
Fig. L |
|
At this point the problem has been solved to three decimal places giving a pretty good idea of how the
technique works. In order to continue just add further pairs of 00 (XX), complete the division and subtract
*half* the squared number as shown above.
The following diagrams take the example to seven decimal places. The process starts from the beginning and shows the soroban after each stage is completed. Use the diagrams as a guide to check accuracy.
THE DIAGRAMS:
Problem: Find the square root of 2
 Fig.1
Fig.1
 Fig.2
Fig.2
 Fig.3
Fig.3
 Fig.4
Fig.4
 Fig.5
Fig.5
 Fig.6
Fig.6
 Fig.7
Fig.7
 Fig.8
Fig.8
 Fig.9
Fig.9
Of course the problem could continue but with 7 decimal places in the answer this is a good place to stop.
Notice rods L through S. At this point they carry the remainder 0.000000088208875. In order to find the true remainder, Kato's technique requires multiplying by 2. Multiply 0.000000088208875 x 2 = 0.00000017641775
The answer is 1.4142135 on rods B through I with a remainder of 0.00000017641775
Square the answer on the soroban
1.4142135 * 1.4142135 = 1.99999982358225
Add the remainder to the squared answer
1.99999982358225
+ 0.00000017641775
2.00000000000000 <=== Answer 2, which is the original problem
- TPH March 2006
18 March, 2006
On a personal note, writing this page 3 months ago required me to seriously examine Prof. Kato's technique. In order to illustrate it I really had to understand it. Since then I've become even more comfortable. I've benefited by routinely practicing using random examples of varying size and typically solving the problem to five or six decimal places. The technique works extremely well and is very efficient. It's well worth taking the time to understand it. In my opinion there is no better method.